- Internal energy is the sum of the randomly distributed kinetic energies and potential energies of the particles in a body.
- The internal energy of a system is increased when energy is transferred to it by heating
- During a change of state, the potential energies of the particle ensemble are changing but not the kinetic energies
- Specific heat capacity: Q = mc ∆ T
- Specific latent heat: Q = mL
- Ideal gas equation: pV = nRT
- Boyle's Law: when temperature is constant
- Charle's Law: when pressure is constant
- Pressure Law: when volume is constant
- Work these out by making the constants and moles k, and see how pressure, temperature and volume relate.
- Absolute zero temperature: -273°C. Lowest possible temperature. Particles have 0 KE, 0 volume, 0 pressure.
- 1 mole has 6.02 x 10^23 particles.
- Work done = pΔV. The area under a pressure-volume graph.
- Brownian motion: random motion of larger particles in a fluid caused by collisions with surrounding particles.
- Kinetic theory assumptions: no intermolecular forces act on the molecules, duration of collisions is negligible compared to time between collisions, random motion of molecules, perfectly elastic collisions, the motion of molecules follow Newton’s laws, the molecules move in straight lines between collisions.
- Moles = mass/ Mr.
- Avogadro constant = 6.02 x 10^23
- Number of particles = Number of moles x Avogadro constant.
- Pressure x volume: pV = nRT = NkT = Nmc2. p: pressure (Pa), V: volume (m3), n: number of moles, N: number of molecules, k: Boltzmann distribution, T: temperature (K), m: mass, c2: mean square speed.
- Kinetic energy of a molecule: E = 3kT/2 = 3nRT/ 2N = 3RT/2NA
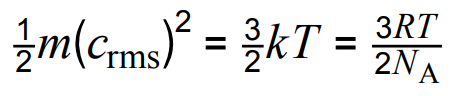
- m: mass (kg), crms: root mean square speed (m/s), k: Boltzmann constant, T: temperature (K), NA: Avogradro, R: 8.31.
- Knowledge and understanding of the behaviour of a gas has changed over time.